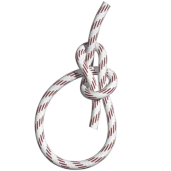Usage
The Snap Bowline is a quick way to tie the Bowline Knot. It is identical in structure to the standard Bowline but is tied in a different manner. The Bowline is used to make a fixed loop in the end of a line. It is relatively easy to untie when not under load. It is commonly used in sailing small craft, for example to fasten a halyard to the head of a sail or to tie a jib sheet to a clew of a jib. The Federal Aviation Administration recommends the Bowline knot for tying down light aircraft. The Bowline should not be used in safety critical applications such as climbing in that it can capsize and/or work itself loose.
Warning
Verify tying technique with a skilled instructor where knot failure could cause property damage, injury, or death.
History
The
Bowline Knot is thought to have been first mentioned in John Smith's 1691 work A Sea Grammar under the name Boling knot. However, the bowline is an ancient knot that has been in use for thousands of years. One instance of use was in the rigging of Egyptian Pharaoh Khufu's solar ship which is believed to be around 2500 years old. The ship (and the bowline) was discovered during a 1954 excavation of the Giza pyramid complex.
Also known as
- Quick Bowline
- Bowline
- Boling Knot
- Bowling Knot
- Standing Bowline
ABOK
Structure
The Snap Bowline is identical to the well-known
Bowline Knot but is tied differently. The final structure of the Snap Bowline is also identical to that of the
Sheet Bend, except the Snap Bowline forms a loop in one rope and the Sheet Bend joins two ropes.
Strength/Reliability
Although generally considered a reliable knot, the Bowline's deficiencies are a tendency to work loose when not under load and the bight portion of the knot to capsize in certain circumstances. To address these shortcomings, a number of more secure variations of the Bowline, such as the
Double Bowline and
Yosemite Bowline, have been developed for use in safety-critical applications. A rope with a Bowline retains approximately 65% of its strength at the location of the knot, although in practice the exact strength depends on a variety of factors.